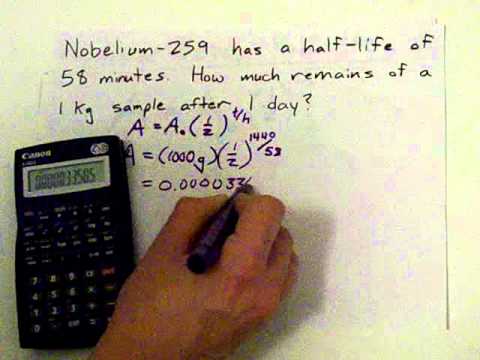How to calculate the half-life
Q. What percent of a sample of CO 60 Half Life 5 years will be left after 25 years?
Figure 11.3. 1 For cobalt-60, which has a half-life of 5.27 years, 50% remains after 5.27 years (one half-life), 25% remains after 10.54 years (two half-lives), 12.5% remains after 15.81 years (three half-lives), and so on.
Table of Contents
- Q. What percent of a sample of CO 60 Half Life 5 years will be left after 25 years?
- Q. What part of titanium would remain after 1 hour?
- Q. What is the half life of Iodine 125 quizlet?
- Q. What percentage of an original sample of iodine-131 will remain after 64 days if Iodine 131 has a half life of 8 days?
- Q. What is the half life of iodine 125?
- Q. What is the half life of uranium 238 quizlet?
- Q. Which is the most susceptible to damage from ionizing radiation?
- Q. What are the half lives of uranium 238?
- Q. How much time will be required for a sample of H 3 to lose 75% of its radioactivity?
- Q. How long will it take the 40 grams of I 131 to decay to approximately 1 100 its original mass?
- Q. What is the half life of Zn 71?
- Q. How do you find half-life examples?
- Q. How does half-life work?
- Q. How much of a sample remains after three half lives have occurred?
- Q. What is half-life and how is it calculated?
- Q. What is the half life symbol called?
- Q. What is the half life of 100?
- Q. Which drug has the longest half-life?
- Q. How many half-lives does it take to clear a drug?
- Q. What is Half-Life Cycle?
- Q. Does a shorter half-life mean more radioactive?
Q. What part of titanium would remain after 1 hour?
What fraction of titanium would remain after one hour? minutes) there are 10 half lives. Therefore the answer is: 9) A medical institution requests 1 g of bismuth-214, which has a half life of 20 min.
- Determine the initial amount of a substance. For example, N(0) = 2.5 kg .
- Determine the final amount of a substance – for instance, N(t) = 2.1 kg .
- Measure how long it took for that amount of material to decay.
- Input these values into our half-life calculator.
Q. What is the half life of Iodine 125 quizlet?
60 days
Q. What percentage of an original sample of iodine-131 will remain after 64 days if Iodine 131 has a half life of 8 days?
As an example, iodine-131 is a radioisotope with a half-life of 8 days. It decays by beta particle emission into xenon-131. After eight days have passed, half of the atoms of any sample of iodine-131 will have decayed, and the sample will now be 50% iodine-131 and 50% xenon-131.
Q. What is the half life of iodine 125?
Q. What is the half life of uranium 238 quizlet?
4.5 billion years
Q. Which is the most susceptible to damage from ionizing radiation?
soft tissue
Q. What are the half lives of uranium 238?
The half-life of uranium-238 is about 4.5 billion years, uranium-235 about 700 million years, and uranium-234 about 25 thousand years.
Q. How much time will be required for a sample of H 3 to lose 75% of its radioactivity?
#9: 100.0 grams of an isotope with a half-life of 36.0 hours is present at time zero. How much time will have elapsed when 5.00 grams remains? #10: How much time will be required for a sample of H-3 to lose 75% of its radioactivity? The half-life of tritium is 12.26 years.
Q. How long will it take the 40 grams of I 131 to decay to approximately 1 100 its original mass?
How long will it take for a 40.0 gram sample of I-131 (half life = 8.040 days) to decay to 1/100 its original mass? 1/100= 0.01. Suppose that n – is number of half lifes, then (1/2)n = 0.01 then n = 6.64. So, the time is 6.64*8.040 = 53.4days.
Q. What is the half life of Zn 71?
2.4 minutes
Q. How do you find half-life examples?
A radioactive half-life refers to the amount of time it takes for half of the original isotope to decay. For example, if the half-life of a 50.0 gram sample is 3 years, then in 3 years only 25 grams would remain. During the next 3 years, 12.5 grams would remain and so on.
Q. How does half-life work?
A medication’s biological half-life refers simply to how long it takes for half of the dose to be metabolized and eliminated from the bloodstream. Or, put another way, the half-life of a drug is the time it takes for it to be reduced by half.
Q. How much of a sample remains after three half lives have occurred?
Three half lives corresponds to (12)3 . So a 18 quantity of the original isotope is retained.
Q. What is half-life and how is it calculated?
The half-life is then determined from the fundamental definition of activity as the product of the radionuclide decay constant, λ, and the number of radioactive atoms present, N. One solves for λ and gets the half-life from the relationship λ = ln2/T1/2.
Q. What is the half life symbol called?
λ
Q. What is the half life of 100?
Half-life (t½) is the amount of time required for a quantity to fall to half its value as measured at the beginning of the time period. In this question (t½) of isotope is 100 years, which means that after 100 years half of the sample would have decayed and half would be left as it is.
Q. Which drug has the longest half-life?
However, there are numerous other drugs with very long half-life, examples are mefloquine 14–41 days (25), amiodarone 21–78 days (26), and oritavancin 393 h (27). Furthermore, what can be called “long half-life” is always relative to the length of the sampling period.
Q. How many half-lives does it take to clear a drug?
Even further, 94 to 97% of a drug will have been eliminated after 4 to 5 half-lives. Thus, it follows that after 4 to 5 half-lives, the plasma concentrations of a given drug will be below a clinically relevant concentration and thus will be considered eliminated.
Q. What is Half-Life Cycle?
Half-life (symbol t1⁄2) is the time required for a quantity to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable atoms survive.
Q. Does a shorter half-life mean more radioactive?
In general there is an inverse relation between the half-life and the intensity of radioactivity of an isotope. Isotopes with a long half-life decay very slowly, and so produce fewer radioactive decays per second; their intensity is less. Istopes with shorter half-lives are more intense.